En noviembre de 2017 se publicó “Los Procesos de Reducción de Tamaño y la Filosofía”¹ y en el 2020 “Estado de Consciencia de un Simulador y el Principio de Causa y Efecto de la Filosofía Antigua”². Con el presente artículo se cierra la trilogía que reúne los procesos de reducción de tamaño con el pensamiento filosófico, proveniente de épocas pretéritas de la humanidad.

Javier Jofré R. Ingeniero Civil Metalurgista, Universidad de Santiago de Chile, Master Business Administration (MBA). Universidad Adolfo Ibáñez, Magister en Filosofía Aplicada, Universidad de los Andes

Platón en la denominada “Alegoría de la Caverna”³ en un diálogo que ocurre entre Sócrates y Glaucón, plantea lo siguiente:

“Represéntate hombres en una morada subterránea en forma de caverna, que tiene la entrada abierta, en toda su extensión a la luz. En ella están desde niños con las piernas y el cuello encadenados, de modo que deben permanecer allí y mirar sólo delante de ellos, porque las cadenas les impiden girar en derredor la cabeza”.

A continuación, Platón dice que estos seres, debido al fuego que está a sus espaldas, están condenados a ver exclusivamente “¿…las sombras proyectadas por el fuego en la parte de la caverna que tienen frente a si”?

Humberto Giannini, en su Breve Historia de la Filosofía⁴ refiriéndose a esta alegoría, expresa: “Por cierto, no es fortuita esta situación; por el contrario, debemos entender que nadie, sino el hombre mismo se ha encadenado a sí a un mundo de sombras (ficticio, ilusorio). La liberación, pues, que es de lo que se trata en el fondo en la alegoría de la caverna, consiste en disponer el alma para el conocimiento del Mundo Real (mundo de las ideas)”.

Lo planteado por cierto también está presente en otras visiones, sean estas religiosas o filosóficas, por ejemplo, en las Enseñanzas del Buda5 se expresa “Ve el mundo como es: una burbuja de jabón, un espejismo…”.

Los procesos de reducción de tamaño y clasificación no están ajenos a esta condición, porque aquello que se logra percibir a través de los sentidos físicos, incluso con el apoyo de sensores, solo permite visualizar una perspectiva fragmentada del mundo exterior y, por lo tanto, en más de una ocasión lo que se logra observar son las sombras proyectadas sobre la pared de la caverna, dejando al observador en la disyuntiva de adjudicarle a lo observado el rótulo de realidad.

A continuación, se presentarán tres casos donde existen causas o efectos ocultos, porque hay efectos que ayudan a ocultar la causa verdadera o porque no todos los efectos que se producen están visibles y se tiende a circunscribirlos a aquellos que resultan ser más evidentes, también puede deberse a causas ocultas que producen efectos visibles o no, también es posible afirmar que es habitual confundir efectos con causas o viceversa, tal vez lo más perturbador es que existen causas y efectos respecto de los cuales no somos conscientes y que contaminan lo que un observador imparcial puede visualizar en aquello que se denomina “realidad”.

Se deja constancia que las causas y efectos podrían identificarse a través de las señales que envía el proceso; éstas requieren ser identificadas y descifradas, el discernimiento ayuda en la identificación, mientras que para conocer su significado es necesaria la sabiduría, la cual tiene, en general, tres componentes: el conocimiento, la experiencia y el deseo consciente de ver más allá de las apariencias a través de la pureza de intención.

CASO 1

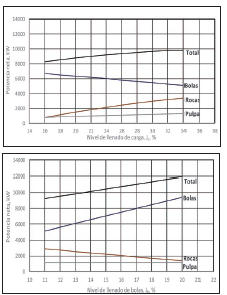
En la molienda SAG, por ejemplo, la demanda neta de potencia se puede desacoplar en la potencia que demandan las rocas, las bolas y la pulpa6, lo cual se observa gráficamente en la Figura 17, donde es posible apreciar la demanda de potencia para cada uno de los componentes de la carga, para un molino de 36 ft x 17 ft (11 m x 5 m), que gira a un 70.4% de la velocidad crítica y tiene un nivel de llenado de bolas, Jb = 12%, un nivel de llenado de pulpa intersticial, Jp = 60%, la gravedad específica del mineral 2.8 t/m3 y el Cp en el molino 65%. Si en lugar de poner en la abscisa el nivel de llenado de carga, Jc, se incorpora como variable independiente el nivel de llenado de bolas, Jb, para un mismo nivel de llenado de carga, Jc = 28%, los efectos asociados se pueden ver en la Figura 2. Se considera en el ejemplo el mismo molino, con las mismas condiciones de operación con las cuales se obtuvo la Figura 1, la única diferencia radica en el cambio de variable independiente de Jc a Jb.

Como se puede observar en ambas figuras, la demanda total de potencia se incrementa en la medida que aumenta el nivel de llenado de carga (Figura 1) para un nivel de llenado de bolas constante y, por otra parte, el incremento de potencia es la respuesta al aumento del nivel de llenado de bolas, para el mismo nivel de llenado de carga (Figura 2).

En la Figura 1 se puede apreciar que la potencia demandada por las bolas disminuye en la medida que aumenta el nivel de llenado de carga y el nivel de llenado de bolas permanece constante, mientras que la potencia que demandan las rocas y la pulpa en el interior del molino aumenta, aunque el incremento de esta última es muy leve comparado con la primera de las mencionadas.

En la Figura 2, se observa lo contrario, la potencia demandada por las bolas aumenta en la medida que se incrementa el nivel de llenado de bolas, mientras que la potencia demandada por las rocas disminuye y la que demanda la pulpa se mantiene constante.

No obstante, aunque en las dos figuras se advierte un incremento de la potencia total, en la medida que aumenta Jc o Jb, ninguna es capaz de responder a la pregunta ¿cuál es la potencia óptima a la cual se debería operar el molino?, considerando solo la variación de los niveles de llenado aparente, Jb y Jc, manteniendo constantes las otras variables de operación y diseño. Aunque en la Figura 2, se advierte una condición más favorable porque la demanda de potencia por parte de las bolas se incrementa en la medida que aumenta Jb, para un Jc constante, lo cual indica que las bolas irán demandando más potencia en la medida que se incremente su presencia en el interior del molino, hasta alcanzar el valor óptimo que maximiza el tonelaje fresco. El análisis de la variación de la potencia para obtener las Figuras 1 y 2 se efectuó con el software Moly-Cop Tools.

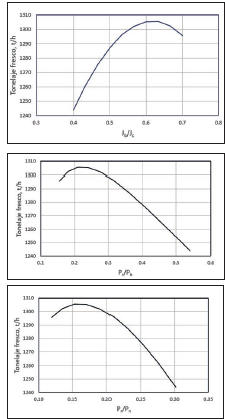
Para responder al interrogante planteado en el párrafo precedente, normalmente se evalúa la variación del tonelaje fresco con la razón Jb/Jc como se puede apreciar en la Figura 3. Se observa que en un extremo el tratamiento disminuye por falta de bolas y en el otro por exceso de éstas, por lo tanto, existe una razón entre ambos niveles de llenado aparente que maximiza el tratamiento de la sección. Dicha razón determina la potencia óptima considerando que el par ordenado (Jb, Jc) tiene asociado un valor de potencia y que, para el máximo tonelaje, se le puede agregar el adjetivo de óptima.

No obstante a lo expresado y aceptando que la causa que provoca la variación de la potencia, que radica en el cambio de Jb para el mismo Jc, encapsulados ambos en la razón Jb/Jc, existe un efecto oculto que en general no se menciona, porque el principal efecto asociado a la maximización del tonelaje fresco logra obnubilar el efecto de la potencia que demandan las rocas y las bolas en el interior del molino, que es muy relevante, porque el tonelaje fresco comienza a disminuir, según este ejemplo en particular, a medida que la potencia que demandan las rocas Pr en el interior del molino, sobrepasa el 21% de la potencia demandada por las bolas, Pb. En este ejemplo en particular, el par ordenado óptimo (Pr, Pb) para la demanda de potencia es (0.21Pb, Pb).

Por supuesto, los valores del par ordenado se modificarán según las variables de operación y diseño consideradas, la naturaleza del mineral y el tipo de circuito, entre otros. Lo expresado se puede observar en la Figura 4. Otra alternativa para expresar lo mismo es con la variación del tonelaje fresco, t/h, con la razón Pr/Pn, que permite visualizar que existe un porcentaje de la potencia que demandan las rocas, de la potencia neta disponible, que configura el óptimo porque maximiza el tratamiento de la sección. En este caso particular corresponde a un 17%.

También se puede expresar cómo la potencia que demandan las bolas, de la potencia neta disponible, que permite optimizar el tratamiento de la sección, corresponde en el ejemplo a un 72%. El 11% restante lo demanda la pulpa presente en el interior del molino, que por cierto no contribuye al proceso de reducción de tamaño, pero que demanda potencia por el solo hecho de estar presente en su interior.

En la Figura 5 se puede observar la variación del tonelaje fresco, t/h. Con la razón Pr/Pn, queda en evidencia que las rocas no pueden ser considerados medios de molienda eficientes, no solo por sus formas irregulares, sino que, por la densidad asociada, que para el caso de minerales de cobre en el ejemplo es 2.8 t/m3, comparado con la densidad de las bolas igual en promedio a 7.75 t/m3.

Todas las simulaciones se efectuaron con los simuladores para la molienda SAG de Moly-Cop Tools, se consideró un circuito en la configuración SABC-1.

En el caso del triturador de cono se utilizó el modelo de Karra8 para simular la granulometría de descarga del triturador, conocidos los parámetros del modelo que utiliza la expresión, que se puede ver en la Ecuación 1.

Donde:

p = Vector granulometría de descarga del triturador.

f = Vector granulometría de alimentación al triturador.

C = Matriz clasificación, matriz diagonal de valores C_ij.

B = Matriz distribución de fractura, matriz triangular inferior de valores B_ij.

I = Matriz identidad.

El simulador de molienda SAG, por su parte, se basa en el modelo general de la molienda expandido para este caso en particular, a través de la función selección específica y distribución de fractura9.

Para la demanda de potencia se utilizó el modelo de Hogg & Fuerstenau¹⁰, que relaciona la demanda de potencia del molino con el diámetro efectivo, la razón (L/D), el porcentaje de velocidad crítica, N_c, el nivel de llenado aparente del molino, J_c, y la densidad aparente de la carga, ρ_apc.

La causa que permanece oculta es la demanda de potencia por parte de las rocas en el interior del molino, porque en la medida que éstas aumentan dicha demanda, llegará a un punto en que se producirá la caída del tonelaje fresco, en el ejemplo, como máximo un 17% de la potencia neta o un 21% de la potencia demandada por las bolas.

Otra causa que permanece oculta en la molienda SAG es la existencia de carga circulante en el interior del molino, la cual es generada por la parrilla interna del equipo, la cual, por ser un clasificador con un tamaño de corte definido por la abertura del slot de la parrilla, inevitablemente generará carga circulante al rechazar aquellas partículas que sean mayores que el tamaño de corte (abertura del slot) de ésta.

La carga circulante interna permanece oculta en el interior del molino, pero se puede reconocer su presencia a través de los efectos que produce, en especial la aparición del denominado proceso de sobrecarga que surge como producto del incremento de la recirculación, porque, por ejemplo, se está procesando un mineral más competente que al molino le resulta más difícil de reducir de tamaño y comienza acumularse en su interior debido a que la parrilla no lo deja salir porque no tiene el tamaño adecuado para abandonar el equipo, o bien, porque se le exige al molino un tonelaje mayor al que puede procesar en las condiciones de diseño y operación imperantes, entre otras condiciones operacionales que posibilitan el incremento de la recirculación interna en el molino.

Se juzga la situación por el efecto, el proceso de sobrecarga, pero la verdadera causa permanece oculta. En el caso de los molinos convencionales de bolas, que tienen descarga por parrilla se observan este mismo tipo de fenómenos.

CASO 2

El modelo de clasificación en hidrociclones desarrollado por CIMM en 1983¹¹ se basa en cinco correlaciones independientes, para la presión, H, tamaño de corte, d₅₀^c, distribución de flujo, S, parámetro de Plitt, m y el by-pass de fino, B_pf, ^°/1, como se puede apreciar en la Ecuación 2.

Si se modifica el ápex (DU), se producen efectos que son bastante conocidos, por ejemplo, se verifican cambios en la presión de alimentación a los ciclones, en el C_p del underflow y, por lo tanto, también en el C_p del overflow, en el B_pw y consecuentemente en el B_pf, la finura del producto del circuito, entre los más conocidos. Sin embargo, existen otros que son menos evidentes, por ejemplo, se modificará el tamaño de corte que hará variar la carga circulante, cambia también la distribución de flujo o carga circulante húmeda, el parámetro de Plitt, la eficiencia de clasificación corregida y, por lo tanto, la eficiencia real de clasificación. Esto trae como consecuencia la modificación del balance en torno a la batería de clasificación, el cual afecta al circuito en su conjunto.

De acuerdo con lo expresado en el párrafo precedente, en el proceso solo se cambió el diámetro del ápex, que en apariencia parece poco significativo; sin embargo, en la práctica se modificó completamente el escenario de la clasificación.

Se debe reconocer, que desde una perspectiva física resulta imposible poder visualizar todos los cambios que se producirán en el proceso, debido a modificaciones en las variables de operación y diseño, por las limitaciones propias de los sentidos físicos y porque en la práctica se observan los efectos superpuestos de varias causas que están actuando al unísono, de las cuales solo se conoce una fracción, por lo tanto, cualquier observador por imparcial que sea, está atrapado al igual que los personajes de la alegoría de la caverna de Platón, viendo las sombras que se reflejan sobre la pared y sin tener otra alternativa que considerar que éstas definen la realidad, al menos, la que se puede distinguir en esas condiciones.

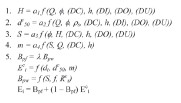
Donde:

H = Presión de alimentación a los ciclones, expresado en pies de pulpa equivalentes.

d₅₀^c= Tamaño de corte corregido, μm.

S = Q_u/Q_o = Distribución de flujo, también conocida como carga circulante húmeda.

m = Parámetro de Plitt, indica la capacidad del ciclón para discriminar entre partículas gruesas y finas, parecidas al tamaño de corte. Corresponde a la pendiente en la zona lineal de la curva de eficiencia corregida, en torno a dc⁵⁰.

B_pf = Fracción de pulpa de alimentación que reporta directamente en el underflow, °/1, cortocircuitando el proceso de clasificación.

(DC) = Diámetro del ciclón, pulgadas.

h = Altura libre del ciclón.

(DI) = Diámetro de entrada, pulgadas.

(DO) = Diámetro del vortex, pulgadas.

(DU) = Diámetro del ápex, pulgadas.

Q = Caudal de pulpa de alimentación al ciclón, m3/h.

f = Fracción de sólido en volumen, en la alimentación al ciclón.

B_pw = By-pass de agua, °/1.

R^c_s = Flujo másico recuperado en el underflow del ciclón corregido, respecto de este mismo en la alimentación a éste, °/1.

E_^ci = Eficiencia de clasificación corregida para partículas de tamaño di.

E_i = Eficiencia real de clasificación para partículas de tamaño di.

a₁, a₂, a₃, a₄ y λ, = Parámetros del modelo.

Si se modifica el diámetro del vortex, el caudal de pulpa (producto de la incorporación de agua al cajón de la bomba) y como consecuencia la fracción de sólido en volumen, en la alimentación a la batería, también se generarán efectos en el escenario de la clasificación en su conjunto y nuevamente, habrá efectos que permanecerán ocultos.

No obstante a lo expresado, los simuladores ayudan a detectar efectos que no son evidentes, porque permiten visualizar los efectos netos, como producto de mover una variable, impidiendo que otros efectos producidos por otras causas, se superpongan a los netos, oscureciendo su detección. Sin desconocer el relevante aporte de los simuladores para develar efectos ocultos, es inevitable la existencia tanto de causas como de efectos, que permanecerán desconocidos, debido a que aquello que se denomina realidad es demasiado rica en acontecimientos.

En la clasificación, generalmente se relaciona el aumento de la presión de alimentación a los ciclones, con una mayor finura en el producto del circuito, lo cual se cumple cuando dicho incremento se debe a una disminución del diámetro del vortex, o bien, al agregar agua al cajón de la bomba, ambos incrementan la presión a la betería y reducen el P80, porque disminuyen el tamaño de corte del clasificador; sin embargo, al disminuir el ápex, también aumentaría la presión pero el P80 aumenta porque se incrementa el tamaño de corte del clasificador.

La presión de alimentación a los ciclones no es una causa, es un efecto al igual que la finura del producto del circuito, por lo tanto, relacionar el incremento de la presión con una mayor finura en el overflow, no siempre es cierto, porque de acuerdo con lo expresado en el párrafo precedente, la presión se puede aumentar sin que el P80 necesariamente disminuya. ¿De qué depende?, de la causa que originó el incremento en la presión de alimentación a la batería.

Cuando se relaciona el incremento de la finura con una mayor presión de alimentación a la batería, el observador está viendo la proyección de las sombras en la pared de la caverna; es decir, está observando lo ilusorio, porque la verdadera causa, que no es la presión, está oculta.

CASO 3

El protocolo definido por Fred C. Bond12 para la determinación del work index se podría decir que es contrario a la molienda, porque ésta se realiza en seco. El nivel de llenado aparente del molino es de 19.42% y su velocidad de 70 rpm, equivalente a 85.7% de la velocidad crítica, en el caso de utilizar la ecuación 3 para determinarla.

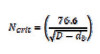
Donde D y d_b, corresponden al diámetro efectivo del molino y de la bola de recarga, respectivamente, en pies. La alta velocidad se justifica porque siendo el molino liso se requiere evitar que la carga de bola resbale en el interior del equipo.

Sin embargo, si se analizan los requisitos especificados por Bond para determinar el work index a escala de laboratorio, lo primero es la molienda en seco, que sin lugar a duda es más ineficiente que la molienda en húmedo; el nivel de llenado aparente del molino de 19.42% está muy por debajo de los niveles que se observan en la operación de molinos industriales; el 85.7% de la velocidad crítica, aunque está por encima de los valores normales a escala industrial, se entiende por la necesidad de levantar la carga del molino liso interiormente.

A esto se debe agregar que Bond definió un molino cuadrado de 12” x 12”. La pregunta evidente es por qué elegir un molino de estas características. En primer lugar, un molino cuadrado tiene una razón L/D igual a 1, con lo cual el efecto de ésta en la demanda de potencia se elimina, además, 12 pulgadas equivalen a 1 pie, por lo tanto, el importante efecto del diámetro en la potencia como se puede observar en la Ecuación 4¹³, pierde toda relevancia. Por otro lado, minimiza el efecto del nivel de llenado solo con un 19.42% de llenado aparente. Agréguese a lo expresado la disminución de la densidad aparente de la carga hasta 4.922 t/m³, al operar con solo un 40.44% de llenado intersticial, debido a que el protocolo estipula la utilización de 700 cm3 de mineral medidos en una probeta graduada de 1,000 cm³.

Donde,

D = Diámetro interno efectivo del molino, pies.

P_net = Potencia neta demandada por el molino, kW.

L = Largo interno efectivo del molino, pies.

N_c = Velocidad de giro, expresada como fracción de la velocidad crítica. °/1.

J = Nivel de llenado aparente, °/1.

a= Ángulo de levante de la carga, °.

En la Figura 6 se presenta la planilla “Mill Power_Ball Mills” de Moly-Cop Tools. En ésta se puede apreciar el cálculo de la potencia para el Molino de Bond, donde se consideró un ángulo de levante de la carga de 45°, porque la evidencia empírica demuestra que en la medida que disminuye el diámetro del molino éste se incrementa

Lo expresado permite afirmar que Fred Bond no quería demandar potencia del motor del molino y que la molienda, por lo tanto, se está efectuando en condiciones que no la favorecen o, en otras palabras, en forma ineficiente como una opción consciente.

Al respecto, surge el interrogante de por qué define Bond un protocolo con el propósito de producir un proceso de molienda muy ineficiente. La respuesta está implícita en la definición de W_i (kWh/tc): “Es la energía necesaria para reducir una tonelada corta de mineral desde un tamaño teóricamente infinito hasta 80% pasante 100 μm¹⁴”, que representa una gigantesca tarea de molienda, que excede con creces cualquier tarea a la cual estará sometido un molino de bolas en la operación industrial, por lo tanto, el W_i correspondería a la máxima energía necesaria para reducir de tamaño un mineral en particular.

En otras palabras, las peores condiciones de operación y diseño asociadas al molino de Bond permiten obtener la máxima energía específica necesaria para reducir de tamaño un mineral, para cumplir con una tarea de molienda extremadamente exigente, esta energía específica se conoce como el work index del mineral.

Lo expresado permite concluir que el work index operacional, obtenido a partir de datos provenientes de la operación en planta, debería ser necesariamente menor que el obtenido a escala de laboratorio, porque en la planta industrial, al contrario de lo que ocurre en el molino de Bond, se busca operar en condiciones de operación y diseño que hagan del proceso de molienda lo más eficiente posible. A esto se debe agregar que la tarea de molienda a escala industrial es significativamente menos exigente que la definida para el W_i obtenido en el molino de laboratorio.

El protocolo de Bond que privilegia una molienda ineficiente se podría identificar como un primer efecto, que busca lograr como segundo efecto el máximo consumo de energía especifica asociado a un mineral en particular, cuya causa original es la excesiva tarea de molienda exigida al proceso de molienda en el laboratorio.

La causa oculta para definir un protocolo, que se opone al proceso de reducción de tamaño en el molino de Bond, es la inmensa tarea de molienda definida por él, para determinar el Wi, donde el tamaño infinito corresponde a una partícula excepcionalmente grande que no tiene un registro energético asociado15. Cualquier otra partícula de menor tamaño debió consumir una cierta cantidad de energía que es desconocida para llegar hasta el tamaño actual, según el primer principio de Bond¹⁶.

CONCLUSIONES

• Existen causas y efectos ocultos en los procesos de reducción de tamaño – clasificación, porque aquello que se denomina realidad es muy rica en acontecimientos.

• Las causas, sin importar si son conocidas o no, producen efectos; algunos de estos se conocen, otros no, pero todos contribuyen a contaminar los efectos netos producto de mover una variable de operación o diseño en una planta industrial.

• En la molienda SAG se acostumbra a buscar la razón óptima de J_b/J_c que permite maximizar el tonelaje fresco del circuito; sin embargo, la verdadera causa (que en general permanece oculta) radica en la demanda de potencia de las rocas, bolas y pulpa en el interior del molino. En el caso de las rocas, en la medida que ésta sobrepasa un 17% de la potencia neta disponible, en el ejemplo desarrollado, comienza a disminuir el tratamiento de la sección. Esto se explica porque las rocas son medios de molienda ineficientes, no solo por sus formas irregulares, sino también por su densidad, 2.8 t/m³ en el ejemplo, significativamente menor que la de las bolas de acero, considerada en promedio de 7.75 t/m³.

En el ejemplo, el máximo tratamiento del circuito SAG está asociado al porcentaje de la potencia neta disponible que demandan las componentes de la carga del molino. Un 17% demandado por las rocas, un 72% que demandan las bolas y el 11% restante por la pulpa.

• La causa principal de la existencia del proceso de sobrecarga en el molino se debe a la carga circulante interna que produce la parrilla del molino SAG. En la medida que ésta aumenta porque el mineral es más competente, o porque se le está exigiendo al molino un tonelaje mayor al que puede procesar en las condiciones de operación y diseño imperantes, entre otras, la recirculación interna se incrementará provocando un proceso de sobrecarga en el molino y la consecuente caída en la demanda de potencia.

Un molino convencional que descarga por parrilla también está expuesto a experimentar procesos de sobrecarga, y como efecto adicional la caída en la demanda de potencia, debido a la carga circulante interna que produce la parrilla en su condición de clasificador con un tamaño de corte asociado.

La carga circulante interna es la causa oculta para la aparición del fenómeno de sobrecarga en molinos que descargan por parrilla, sean estos SAG o convencionales. Al aumentar la carga circulante, aumenta el nivel de llenado de carga, el brazo del torque y éste último disminuye y la demanda de potencia cae.

• En el proceso de clasificación en hidrociclones, se tiende a relacionar el incremento de la presión de alimentación a la batería con la finura de producto en el rebose del equipo. Sin embargo, la presión es un efecto, no una causa. Si se cierra el vortex o el ápex o se incrementa el caudal de pulpa de alimentación a la batería, entre otros, la presión experimentará un aumento. En el caso de la disminución del diámetro del vortex y el aumento del caudal de pulpa, junto con el incremento de la presión, se obtendrá un producto más fino, pero al cerrar el ápex, a pesar de producirse un aumento en la presión, el producto del rebose del hidrociclón se engrosará, porque aumentará el tamaño de corte del equipo.

Cuando se relaciona el incremento de la finura con una mayor presión de alimentación a la batería, el observador está viendo la proyección de las sombras en la pared de la caverna; es decir, está observando lo ilusorio, porque la verdadera causa que no es la presión permanece oculta.

• Un cambio en apariencia insignificante en la denominada realidad física podría provocar cambios trascendentes en el proceso. Por ejemplo, si se modifica el diámetro del ápex, según la Ecuación 2, produciría un cambio en la presión de alimentación a la batería, en el tamaño de corte, en el Split de flujo, en el m de Plitt, en la eficiencia corregida E_i^c, en el R_c^s, en el B_pw, en el B^pf y en la eficiencia real de clasificación E_i, por lo tanto, un simple cambio de ápex produciría un cambio completo en el escenario de la clasificación. Este cambio de escenario provocará una modificación en el balance en torno a la batería de clasificación, que repercutirá en el circuito en su conjunto.

Una causa en apariencia insignificante produce un sinnúmero de efectos, algunos visibles y otros que permanecen ocultos y que solo se pueden develar en parte con la ayuda de los simuladores.

La verdadera “reacción en cadena” de cambios que se produce por el solo hecho de modificar el ápex o el vortex o el caudal de pulpa de alimentación a la betería de clasificación no es posible observarlos en la planta, porque están ocurriendo una serie de fenómenos simultáneos que están provocando causas que generan efectos que contaminan los efectos netos que permite observar el simulador, manifestándose con mayor énfasis lo ilusorio que define Platón en la “Alegoría de la Caverna”.

• El protocolo definido por Fred Bond para la determinación del W_i a escala de laboratorio, es contrario a un proceso de molienda eficiente, porque busca determinar la energía especifica necesaria para efectuar una tarea de molienda gigantesca, desde un tamaño teóricamente infinito hasta 80% pasante 100 μm, por lo tanto, el Wi estimado en el molino de Bond debería considerarse como la máxima energía específica, kWh/t_c, necesaria para reducir de tamaño un mineral en particular.

En otras palabras, la causa oculta para que Fred Bond haya definido un protocolo contrario a un proceso de molienda eficiente a escala de laboratorio radica en la definición del W_i (kWh/t_c), obteniéndose como efecto adicional que éste sea la máxima energía específica necesaria para reducir de tamaño un determinado mineral en la molienda de bolas convencional.

Un primer corolario, que se desprende de lo expresado en el párrafo precedente, es que el W_i de la operación, W_i,Op, debería ser menor que el W_i obtenido en el laboratorio, porque en la planta se está haciendo todo lo posible para que el proceso de molienda en molinos de bolas se verifique en forma eficiente. Si el W_i,Op, es mayor que el obtenido en el laboratorio, es una evidencia que en la planta hay un espacio abierto para mejorar el desempeño del proceso.

• La “Alegoría de la Caverna” de Platón plantea la existencia de una componente ilusoria en la vida, que Humberto Giannini explica que son los propios seres humanos quienes se han encadenado a un mundo ficticio e ilusorio. Por cierto, los procesos de reducción de tamaño y clasificación no están ajenos a este fenómeno, por esa razón resulta complejo visualizar los efectos netos en la realidad física, debido a la existencia de causas y efectos ocultos, pero también al otorgar el estatus de causa a efectos o viceversa. Sin embargo, los simuladores son una herramienta importante que ayuda a despejar en parte la componente ilusoria a la que el género humano está expuesto durante su existencia.

AGRADECIMIENTOS

El autor agradece muy sinceramente a todos los colegas que tuvieron la gentileza de contribuir con sus valiosos comentarios a enriquecer este artículo: Juan Luis Bouso, Gabriel Berkowitz, Juan Carlos Tapia, Marcelo Jo, Luis Castro, Sandro Marino, Cristian Alvayai, Antonio Fuentes, Luis Silva y Milton Rojas.

REFERENCIAS

Bond, F. C., “Crushing & Grinding Calculations Part I”, British Chemical Engineering, Vol. 6, N° 6, pp. 378 – 385, 1961.

Giannini, H., “Breve Historia de la Filosofía”, Catalonia Ltda., Santiago de Chile, 2005.

Gutierrez, L., Sepúlveda, J. E., “Dimensionamiento y Optimización de Plantas Concentradoras Mediante Técnicas de Modelación Matemática”, Centro de Investigación Minera y Metalúrgica, CIMM, Santiago de Chile, 1986.

Hogg, R., Fuerstenau, D. W., “Power Relationships for Tumbling Mills”, Trans. SME-AIME, Vol. 252, pp. 418 – 432, 1972.

Jofré, J., “Los Procesos de Reducción de Tamaño y la Filosofía”, revista Rocas y Minerales, página 66 – 75, año XLV, número 547, noviembre 2017, España.

Jofré, J., “Estado de Consciencia de un Simulador y el Principio de Causa y Efecto de la Filosofía Antigua”, revista Rocas y Minerales, página 60 – 75, año XLVIII, número 577, julio-agosto 2020, España.

Menacho, J., Jofré, J., Zivcovic, J., “Tópicos Especiales de Conminución de Minerales”, Programa Iberoamericano de Ciencia y Tecnología para el Desarrollo, CYTED, 1995.

Platón, “Diálogos IV, República”, Editorial Gredos S.A., Madrid, España, 1988.

Sepúlveda, J.E., “Un Modelo Fenomenológico de la Molienda Semiautógena (en Ambiente Moly-Cop Tools)”, III Simposio Internacional de Mineralurgia, TECSUP, Lima, Perú, agosto 9 – 11 de 2000.

Versión Blanco, A., “El Dhammapada, las enseñanzas del Buda”, Editorial Troquel S.A., Buenos Aires, Argentina, 1995.

1[Jofré, J., 2017, 66]
2 [Jofré, J., 2020, 60]

3 [Platón, 1988, 338]
4 [Giannini, 2005, 52]

5 [El Dhammapada, 1995, 56]
6 [Sepúlveda, J. E., 2000, 10
7 [Sepúlveda, J. E., 2000, 12]
8 [Menacho, J., Jofré, J., Zivcovic, J., 1995, 2 – 36],
9 [Sepúlveda, J. E., 2000, 14-15],
10 [Hogg, R., Fuerstanau, D., 1972, 6 pp.]
11 [Gutierrez, L., Sepúlveda, J. E., 1986, 173]

12 [Bond, F.C., 1961, 382]
13 [Opus Cité 10.]
14 [Opus Cité 12.]

15 [Bond, F. C., 1961, 382]
16 [Ibidem]

Información de Fueyo Editores